分類法では、まずオフラインにて分類を実行するための分類器を用意します。 分類器の作成は大きく分けて、特徴量の抽出⇒情報の追加⇒トレーニングの3つのステップに分かれます。

1. 特徴量の抽出：
正しい分類結果が既知の画像セットを用意し、これらの画像から特徴量を抽出します。特徴量とは、丸さや面積値、輝度値など、品種を特定する上で必要な情報のことを指します。

2. 情報の追加：
答えとなる分類番号とともに、取得した特徴量を分類器に追加することで、「このクラスのときにはこういった特徴がある」ということをHALCONに覚えこませていきます。

3. トレーニング：
与えられた情報に対して正しい分類結果が得られるように繰り返し演算が行われ、各クラス間の境界線が算出されます。

オンラインの検査時には、分類器を作成する際に抽出したものと全く同じ特徴量を検査画像から取得し、これをオフラインで作成した分類器に入力することでクラスの自動判定が行われます。

図1. 分類法の処理の流れ

■ 適切な特徴量の選択

画像を見ると、1つのクラスの中でも様々な向きや大きさを持つことが確認できます。分類法でよく使われる特徴量として面積値（area_center()で取得可能）が挙げられますが、今回のようなケースではクラスの特徴を的確に表す値とは言えず、逆に分類精度を引き下げる方向に働く可能性があります。 今回は、例えば下記のような向き/大きさに依存しない特徴量が有効です。

- Circularity: 真円度 (circularity()にて取得可能)
ピンホールのような円形状のものに対しては1に近い値、それ以外では低い値を示す

- Anisometry: 縦横比: (eccentricity()にて取得可能)
糸くずのような線形状では高い値、ピンホールのような円形状では1に近い値を示す

- Convexity: 凸面度: (convexity()にて取得可能)
異物のような凹凸の多いものでは低い値、ピンホールなどの凹凸のない形状では1に近い値を示す

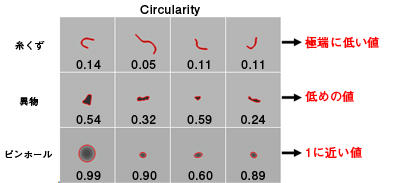
図3. 特徴量'Circularity'に対する各クラスの傾向

■ ユーザー定義の特徴量（応用編）

また、関数を複数組み合わせて、ユーザー定義の新たな特徴量を作るのも有効です。

例えば、領域の距離変換を行う ditance_transformation() と 領域の骨格線を取得する skelton()、輝度の平均/分散を取得する intensity() の3つを組み合わせることで、領域の骨格線から境界線までの距離の平均と分散を取得することが可能です。

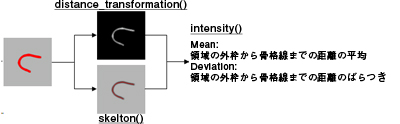
図4. ユーザー定義の特徴量: 領域の外枠から骨格線までの距離

糸くずなどの一様な細い線状の欠陥は、Mean/Deviationともに小さな値が得られるのに対し、異物などの形状が安定しない欠陥は、Deviationの値が大きくなります。また、一様な円形状のピンホールはDeviationが小さいという特徴が得られます。

図5. 領域の外枠から骨格線までの距離のばらつきの各クラスの傾向

これらの全ての特徴量それぞれに対して、適切なしきい値を試行錯誤で求めるのは非常に膨大な時間と手間を要しますが、分類法を使用するのであれば、上記の関数で特徴量を抽出して分類器に情報を追加するだけです。後はHALCONが自動で適切な分類を行います。

高機能がゆえに敬遠されがちですが、実は非常に扱いやすく簡単な機能の1つです。欠陥分類だけでなく、例えば製品の仕分けなど、種類が多い場合には無数の条件分岐を強いられ、プログラムが繁雑になりがちですが、分類法ですっきりさせてしまうのも1つの手です。

上記の手法を実装したサンプルプログラムが下記からダウンロードしていただけます。

上記で示した特徴量以外にも様々な特徴量を使用しています。プログラムを実際に触りながら、他にどのような特徴量が有効かなどを検討してみるのも面白いかもしれません。

・検査画像枚数：30枚（各クラス10枚ずつ） ・トレーニング用画像：12枚（各クラス4枚ずつ） ・分類結果：30/30（正しく分類された枚数/検査画像枚数） この事例のサンプルプログラムをダウンロード